OIT (Order Independent Transparency)

1. Alpha Channel

Porter proposed the "Alpha channel"(1.[Porter 1984]) in 1984 which is widely established in real-time rendering to simulate the transparent effect.

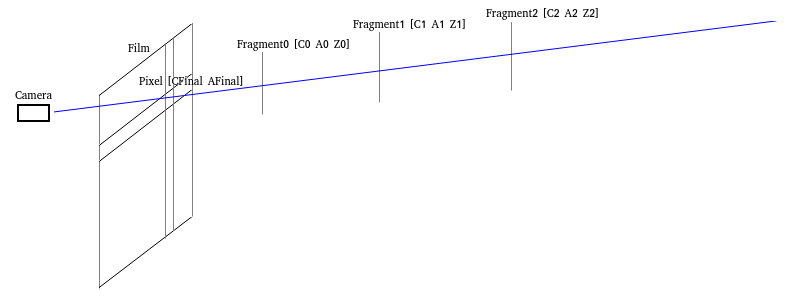
We assume that one "pixel" corresponds to a series of "fragments" which can be treated as the triples $\displaystyle \begin{bmatrix} C_i & A_i & Z_i \end{bmatrix}$ (C-Color A-Alpha Z-Depth), as shown in the following figure:

Then the final color of the pixel can be calculated as $\displaystyle C_{\displaystyle Final} = \sum_{\displaystyle i = 0}^{\displaystyle n} (\prod_{\displaystyle Z_j Nearer Z_i}(1 - A_j)) A_i C_i$ .

The $\displaystyle \operatorname{V} ( Z_i ) = \prod_{\displaystyle Z_j Nearer Z_i} 1 - A_j$ is also called the visibility function which will be explained later.
Then the above equation can also be written as $\displaystyle C_{\displaystyle Final} = \sum_{\displaystyle i = 0}^{\displaystyle n} \operatorname{V} ( Z_i ) A_i C_i$ .

Note that the physical meaning of the Alpha is the "partial coverage" rather than the "transmittance".

The Alpha stands for the ratio of the area covered by the fragments to the area covered by the pixel. That's why we use the scalar "float" instead of the vector "RGB" to represent the Alpha. This circumstance is also called the "Wavelength Independent" in some literatures.
For example, when we observe a red brick through a blue silk scarf, the color of the brick appears to be the "addition" of the blue and red. The fibers of silk scarf are intrinsically opaque but there exist gaps between the fibers. We see the brick through the gaps. Namely, the silk scarf "partially covers" the brick.

However, the transmittance is "Wavelengh Dependent". If we observe a red brick through a blue plastic film, the color of the brick appears to be black (the "Multiplication" of the blue and red). The red brick only reflects the red light while the blue plastic film only allows blue light to pass through. All the reflected light of the red brick is absorbed by the blue plastic film and then the red brick appears to be black.

You can do the above two experiments by yourself.

If we demand the transmittance effect, the techniques related to the "Participating Media"(2.[Yusor 2013]、3.[Hoobler 2016]) should be used.

By the physical meaning of the Alpha, we can comprehend the visibility function $\displaystyle \operatorname{V} ( Z_i )$ evidently since a fragment can only be (partially) covered by the fragments nearer than it.
Some literatures treat the visibility function $\displaystyle \operatorname{V} ( Z_i )$ as the "transmittance". Technically, that's wrong.

2. Ordered Transparency

In real time rendering, the classic method is to sort the transparent geometries and use the "Over/Under Operation"(1.[Porter 1984]、4. [Dunn 2014]) to calculate the final color $C_{Final}$ recursively:

1.OpaquePass
draw the opaque geometries and have the BackgroundColor and the BackgroundDepth.

2.TransparencyPass
use the BackgroundDepth for depth test (without depth write), sort the geometries from far to near/from near to far and use Over/Under Operation to calculate recursively.

Over Operation
sort the fragments from far to near to use the Over Operation
$C_{Final\_0}=BackgroundColor$
$C_{Final\_n}=(A_nC_n)+(1-A_n) C_{Final\_n-1}$

Under Operation
sort the fragments from near to far to use the Under Operation
$C_{Final\_0}=0$
$A_{Total\_0}=1$
$C_{Final\_n}=A_{Total\_n-1}( A_nC_n)+C_{Final\_n-1}$
$A_{Total\_n}=A_{Total\_n-1}( 1-A_n)$
Note that the $A_{Total}$ in Under Operation is exactly the visibility function $\operatorname{V} ( Z_i )$ above.
At last, the result image of the OpaquePass is treated as the fragments with "A=1 C=BackgroundColor" and added to the final color by the Under Operation.

By the mathematical induction, we can prove that the Over Operation and the Under Operation are equivalent. Both can calculate the final color $C_{Final}$ correctly by $\displaystyle \sum_{\displaystyle i = 0}^{\displaystyle n} \operatorname{V} ( Z_i ) A_i C_i$ .

Technically, the correctness of the Over/Under Operation can only be guaranteed by sorting the "fragments" from far to near/from near to far. However, in real time rendering, the sorting is based on the geometries not the fragments. If there exists interlacing inside the geometry, the order of the fragments will not follow and thus we have to explore the OIT(Order Independent Transparency) algorithm to settle this problem.

Note that keeping the geometries orderly also prohibits the batching of the geometries with the same material and thus results in extra state changing which is hostile to the performance.

3-1. Depth Peeling

Depth Peeling(5.[Everitt 2001]) is an archaic method which might be used in real time rendering.

3-1-1. Render Pass

1.OpaquePass
draw opaque geometries and have the BackgroundColor and the BackgroundDepth.

2.NearestLayerPass //GeometryPass
copy the BackgroundDepth to initialize the depth buffer
with depth test(NearerOrEqual) and depth write, sort the transparent geometries by [material, front-to-back] and draw them, having the NearestLayerColor and the NearestLayerDepth
add the NearestLayerColor to the final color $C_{Final}$ by Under Operation
//Note that the depth peeling doesn't depend on the order of the fragments and we sort the geometries from near to far is merely to improve the performance by the EarlyDepthTest.

3.SecondNearestLayerPass //GeometryPass copy the BackgroundDepth to initialize the depth buffer
with depth test(NearerOrEqual) and depth write, sort the transparent geometries by [material, front-to-back], bind the NearestLayerDepth to the SampledTextureUnit and draw them with discarding the fragments NearerOrEqual than the NearestLayerDepth explicitly in the fragment shader, having the SecondNearestLayerColor and the SecondNearestLayerDepth
add the SecondNearestLayerColor to the final color $C_{Final}$ by Under Operation
//Note that the depth peeling doesn't depend on the order of the fragments and we sort the geometries from near to far is merely to improve the performance by the EarlyDepthTest.

4.ThirdNearestLayerPass //GeometryPass copy the BackgroundDepth to initialize the depth buffer
with depth test(NearerOrEqual) and depth write, sort the transparent geometries by [material, front-to-back], bind the SecondNearestLayerDepth to the SampledTextureUnit and ...
//Note that the depth peeling doesn't depend on the order of the fragments and we sort the geometries from near to far is merely to improve the performance by the EarlyDepthTest.

The subsequent operations are similar to the above, omitted... //we can peel N layers by N geometry passes. The application can choose the proper N according to the requirements.

N+2.CompositePass //FullScreenTrianglePass
At last, the BackgroundColor by OpaquePass is added to the final color by the Under Operation.

Technically, it's legal to peel the layers from far to near and add them to the final color by the Over Operation.
However, if the number of the geometry passes N is too low to peel all layers, the farthest/nearest layers will be ignored when we use the Under/Over Operation.
Evidently, the visibility function $\displaystyle \operatorname{V} ( Z_i )$ is monotonically decreasing. It follows that the farthest layers generally contribute little to the final color and introduce little error if they are ignored. That's why we prefer the Under Operation to the Over Operation.

3-1-2. Conclusion

Evidently, the depth peeling has a fatal disadvantage that the number of the geometry passes is too high and the performance is too low and thus the depth peeling has never been popular since proposed decades ago.

3-2. Stochastic Transparency

The estimation of the visibility function $\displaystyle \operatorname{V} ( Z_i )$ depends on the order of the fragments. This results in that the estimation of the final color $\displaystyle C_{\displaystyle Final} = \sum_{\displaystyle i = 0}^{\displaystyle n} \operatorname{V} ( Z_i ) A_i C_i$ depends on the order.
By this fact, Enderton proposed the "stochastic transparency"(6.[Enderton 2010]) in 2010 which is based on the the principles of statistics and uses MSAA hardware to random sampling to estimate the visibility function $\operatorname{V} ( Z_i )$ order independently.

3-2-1. Stochastic Depth

With the MSAA on, we assume the relationship among the "pixel", "fragment" and "sample" as the following figure:

one pixel corresponds to several samples (for example, in the above figure, one pixel corresponds to 4 samples, namely, 4X MSAA) and at the same time one pixel corresponds to a series of fragments.
However, the same sample corresponding to the same pixel can only be occupied by one fragment of these fragments corresponding to the same pixel(The storage is limited, which can hold only one fragment. That's evident).

At the same time, we assume that:
$Z_j$ denotes one fragment of the fragments$Z_0$ $Z_1$ $Z_2$ ... $Z_n$ corresponding to the same pixel.
$Z_s$ denotes the fragment which occupies the sample in the final result depth image(the StochasticDepth in the implementation). As we have explained above, by the limit of the storage, the sample can only be occupied by one fragment.
$Z_i$ denotes the fragment which is being discussed(which can be considered as the fragment being executed by the fragment shader in the implementation).

In addition, we assume that:
By setting the value of gl_SampleMask/SV_Coverage, we ensure that the probability of each sample be occupied by the fragment [ $C_i$ $A_i$ $Z_i$ ] is $A_i$ .
With depth test and depth write, we ensure that the nearer fragment must overwrite the farther fragment and the sample is occupied by the nearest fragment.
The probabilities of different fragments are uncorrelated.

We claim that for each sample [ $C_s$ $A_s$ $Z_s$ ] in the final result depth image, for each fragment [ $C_i$ $A_i$ $Z_i$ ] among the fragments corresponding to the same pixel, the probability of "$Z_i$ is Near-or-Equal than $Z_s$ " is exactly the visibility function $\displaystyle \operatorname{V} ( Z_i ) = \prod_{\displaystyle Z_j Nearer Z_i} 1 - A_j$ .

Proof:
Since "the nearer fragment must overwrite the farther fragment", if "$Z_i$ is Near-or-Equal than $Z_s$ ", then we have that the sample in the final result depth image is occupied by [ $C_i$ $A_i$ $Z_i$ ] or the farther fragments corresponding to the same pixel.
Namely, the sample is not be occupied by the nearer fragments corresponding to the same pixel.
Evidently, the probability of "the sample is not be occupied by one fragment $Z_j$ among these nearer fragments" is $1 - A_j$ .
Since "the probabilities of different fragments are uncorrelated", by the multiplication principle, the probability of "the sample is not be occupied by the nearer fragments corresponding to the same pixel" is $\displaystyle \prod_{\displaystyle Z_j Nearer Z_i} 1 - A_j$ which is exactly the visibility function $\displaystyle \operatorname{V} ( Z_i )$.

Besides, we assume that:
One pixel corresponds to S samples, namely, S-X MSAA.

We claim that if the count of the samples such that "$Z_i$ is Near-or-Equal than $Z_s$ " is $\operatorname{Count} ( Z_i )$, let $\displaystyle \operatorname{SV}( Z_i ) = \frac{ \operatorname{Count} ( Z_i ) }{S}$, we have that the expected value of the $\displaystyle \operatorname{SV}( Z_i )$ is the visibility function $\displaystyle \operatorname{V} ( Z_i )$.

Proof: Evidently, this is immediate from the above proposition.

Since we can get the value of $\operatorname{Count} ( Z_i )$ by sampling texture, we can use $\displaystyle \operatorname{SV}( Z_i )$ to estimate the visibility function $\displaystyle \operatorname{V} ( Z_i )$ .
Note that the extension "ARB_texture_multisample" should be enabled to use texelFetch on sampler2DMS in OpenGL.
We should use the knowledge of statistics to prove why we can estimate and thus the proof is omitted.

3-2-2. Alpha Correction

We claim that ${\displaystyle{\sum_{i = 0}^n}} ( \operatorname{V} ( Z_i ) A_i ) = 1 - {\displaystyle{\prod_{i = 0}^n}} ( 1 - A_i )$.

Proof:
Prove by the mathematical induction.
1.basis:
when n=0:
left = ${\displaystyle{\sum_{i = 0}^0}} ( \operatorname{V} ( Z_i ) A_i )$
= $\operatorname{V} ( Z_0 ) A_0$
= $1 \cdot A_0$
= $A_0$
right = $1 - {\displaystyle{\prod_{i = 0}^0}} ( 1 - A_i )$
= $1 - ( 1 - A_0 )$
= $A_0$
left = right the equation holds
2.inductive step:
we assume that the proposition holds for n=k.
when n=k+1:
left = ${\displaystyle{\sum_{i = 0}^{k + 1}}} ( \operatorname{V} ( Z_i ) A_i )$
= ${\displaystyle{\sum_{i = 0}^k}} ( \operatorname{V} ( Z_i ) A_i ) + \operatorname{V} ( Z_{k+1} ) A_{k+1}$
= $1 - {\displaystyle{\prod_{i = 0}^k}} ( 1 - A_i ) + \operatorname{V} ( Z_{k+1} ) A_{k+1}$
= $1 - {\displaystyle{\prod_{i = 0}^k}} ( 1 - A_i ) + ( {\displaystyle{\prod_{i=0}^k}} ( 1 - A_i ) ) \cdot A_{k+1}$
= $1 - ( {\displaystyle{\prod_{i = 0}^k}} ( 1 - A_i )) \cdot ( 1 - A_{k+1} )$
= $1 - {\displaystyle{\prod_{i = 0}^{k + 1}}} ( 1 - A_i )$
right = $1 - {\displaystyle{\prod_{i = 0}^{k + 1}}} ( 1 - A_i )$
left = right the equation holds

Evidently, the expected value of ${\displaystyle{\sum_{i = 0}^n}} ( \operatorname{SV} ( Z_i ) A_i )$ is ${\displaystyle{\sum_{i = 0}^n}} ( \operatorname{V} ( Z_i ) A_i )$.
Since ${\displaystyle{\sum_{i = 0}^n}} ( \operatorname{V} ( Z_i ) A_i ) = 1 - {\displaystyle{\prod_{i = 0}^n}} ( 1 - A_i )$, we have that the expected value of ${\displaystyle{\sum_{i = 0}^n}} ( \operatorname{SV} ( Z_i ) A_i )$ is $1-\prod_i ( 1-A_i )$.

The Alpha correction can be considered as the normalizing of the $\operatorname{SV} ( Z_i )$.
This means that we assume that $\frac{\operatorname{SV} ( Z_i )}{ {\displaystyle{\sum_{i = 0}^n}} ( \operatorname{SV} ( Z_i ) A_i )} = \frac{\operatorname{V} ( Z_i )}{ {\displaystyle{\sum_{i = 0}^n}} ( \operatorname{V} ( Z_i ) A_i ) }$ and we have that ${\operatorname{V} ( Z_i )} = {\operatorname{SV} ( Z_i )}{\frac{ {\displaystyle{\sum_{i = 0}^n}} ( \operatorname{V} ( Z_i ) A_i ) }{ {\displaystyle{\sum_{i = 0}^n}} ( \operatorname{SV} ( Z_i ） A_i ）}} = { \operatorname{SV}( Z_i )}{\frac{1 - {\displaystyle{\prod_{i = 0}^n}} ( 1-A_i )}{ {\displaystyle{\sum_{i = 0}^n}} ( \operatorname{SV} ( Z_i ) A_i )}}$.

We should use the knowledge of statistics to explain the meaning of the Alpha correction and thus the explanation is omitted.

3-2-3. Render Pass

1.OpaquePass
draw the opaque geometries and have the BackgroundColor and the BackgroundDepth.

2.StochasticDepthPass //GeometryPass
copy the BackgroundDepth to initialize the depth buffer
with MSAA, with depth test(NearerOrEqual) and depth write, sort the transparent geometries by [material, front-to-back] and draw them with setting the pseudo random value of gl_SampleMask/SV_Coverage by the $A_i$ of [ $C_i$ $A_i$ $Z_i$ ], having the StochasticDepth
Note that:
2-1.The stochastic transparency doesn't depend on the order of the fragments and we sort the geometries from near to far is merely to improve the performance by the EarlyDepthTest.
2-2.Turning on MSAA in StochasticDepthPass is to random sample and the stochastic transparency intrinsically doesn't demand other passes to turn on the MSAA.
If the application demands the effect of "Spatial AntiAliasing", the application can turn on MASS in other passes(Evidently, the application use arbitrary algorithms(for example, the FAXX) in other passes).
These's no relationship between the MSAA used for random sampling (in StochasticDepthPass) and the MSAA used for spatial antialiasing (in other passes). For example, we can use 8X MASS in StochasticDepthPass while use 4X MSAA in other passes.
2-3.To ensure the uncorrelation among fragments, we must use pseudo random value rather than the "AlphaToCoverage" hardware feature.
2-4.The depth value used in AccumulatePass is the value of the shading position not the value of the sampling position. To be consistant, we prefer to write the depth (value of the shading position) to gl_FragDepth/SV_Depth in the fragment shader.
2-5.By the limit of the hardware, the maximum sample count of MSAA is 8X MSAA. The author (6.[Enderton 2010]) proposed that we can use multiple passes to simulate more sample counts. Due to the performance issue, we only use one pass.

3.AccumulateAndTotalAlphaPass //GeometryPass
copy the BackgroundDepth to initialize the depth buffer
with depth test without depth write, with MRT and SeparateBlend/IndependentBlend, sort the transparent geometries by [material], bind the StochasticDepth to the SampledTextureUnit and draw them with estimate $\operatorname{SV} ( Z_i )$ by sampling the texture in fragment shader, having the StochasticColor, CorrectAlphaTotal and StochasticTotalAlpha
Note that:
3-1.Since the depth write is turned off, the order of the geometries doesn't impact on the performance and thus we sort the geometries only by the material.
3-2.We have that "StochasticColor = ${\displaystyle\sum_{i = 0}^n} \operatorname{SV} ( Z_i ) A_i C_i$ ", "CorrectAlphaTotal = $1 - {\displaystyle\prod_{i = 0}^n} ( 1 - A_i )$" and "StochasticTotalAlpha = ${\displaystyle\sum_{i = 0}^n} ( \operatorname{SV} ( Z_i ) A_i )$".
3-3.The relationship between the AlphaTotal and the TotalAlpha is TotalAlpha = 1 – AlphaTotal. The term "TotalAlpha" is from the stochastic transparency(6.[Enderton 2010]) while the term "AlphaTotal" is from the Under Operation(1.[Porter 1984]、4. [Dunn 2014]).
3-4.The StochasticTotalAlpha is only used when the Alpha correction is turned on. This means that we can reduce one RT if we don't turn on the Alpha correction.
3-5.The author(6.[Enderton 2010]) use two separate passes AccumulatePass(which calculates the StochasticColor and the StochasticTotalAlpha) and TotalAlphaPass(which calculates CorrectAlphaTotal). However, we can totally merge them into a single pass. Maybe the SeparateBlend/IndependentBlend was not supported by the hardware when the author published the paper.

4.CompositePass //FullScreenTrianglePass
Without the Alpha correction, the total contribution of the transparent geometries:
TransparentColor = $\displaystyle { \sum_{i = 0}^n} \operatorname{SV} ( Z_i ) A_i C_i$ = StochasticColor
With the Alpha correction, the total contribution of the transparent geometries:
TransparentColor = ${\begin{cases} {\displaystyle\sum_{i = 0}^n} { ( \operatorname{SV} ( Z_i ) \frac{1- {\displaystyle\prod_{i = 0}^n} ( 1 - A_i ) }{ {\displaystyle\sum_{i = 0}^n} ( \operatorname{SV}( Z_i ) A_i )} ) A_i C_i } &{if \; {\displaystyle\sum_{i = 0}^n} {\operatorname{SV}( Z_i ) A_i)} > 0} \\0 &{if \; {\displaystyle\sum_{i = 0}^n} \operatorname{SV}( Z_i ) A_i = 0} \end{cases}}$
= ${\begin{cases} {({\displaystyle\sum_{i = 0}^n}{\operatorname{SV}( Z_i )} A_i C_i)}{\frac{1 - {\displaystyle\prod_{i = 0}^n}( 1 - A_i )}{{\displaystyle\sum_{i = 0}^n}(\operatorname{SV}( Z_i ) A_i)}} &{if\;{\displaystyle\sum_{i = 0}^n} ( \operatorname{SV}( Z_i ) A_i ) > 0} \\0 &{if\;{\displaystyle\sum_{i = 0}^n}{({\operatorname{SV}( Z_i)}A_i)}=0} \end{cases}}$
= ${\begin{cases} \text{StochasticColor} \frac{ 1 - \text{CorrectAlphaTotal}}{\text{StochasticTotalAlpha}} &{if\;{\displaystyle\sum_{i = 0}^n}{({\operatorname{SV}( Z_i )}A_i)} > 0} \\0 &{if\;{\displaystyle\sum_{i = 0}^n} ( \operatorname{SV}( Z_i ) A_i ) = 0} \end{cases}}$
Note that the StochasticTotalAlpha of opaque geometries is evidently zero. However, due to the random sampling, the StochasticTotalAlpha of the transparent geometries can be zero as well.

Then, add the TransparentColor to the final color $\displaystyle C_{Final}$ by the Over Operation:
$\displaystyle C_{Final}$ = TransparentColor + CorrectAlphaTotal × BackgroundColor
Note that the BackgroundColor has been added to the color buffer. We can output the TransparentColor and CorrectAlphaTotal in the fragment shader and use the Alpha blend hardware feature to implement the Over Operation.

3-2-4. Tile/On-Chip Memory

The stochastic transparency is intrinsically suitable to mobile GPU.

In the traditional desktop GPU, the performance bottleneck is the MSAA. Since one pixel corresponds to S samples, the bandwidth is increased by S times.

However, in the mobile GPU, this problem has been solved effectively. We can keep the MSAA image in the Tile/On-Chip Memory and discard the MSAA image when the renderpass ends without writing to the main memory. This means that the bandwidth can be decreased to almost zero.

The Vulkan/Metal API allows the application to set this configuration explicitly:
Use the "VK_IMAGE_USAGE_TRANSIENT_ATTACHMENT_BIT"/"MTLStorageModeMemoryless" to set the storage mode of the image to the Tile/On-Chip Memory explicitly.
And the images with this storage mode prohibit to be read by the traditional sampled texture unit in the fragment shader and must be read by the "Subpass Input"/"[color(m)]Attribute".

The OpenGL API doesn't allow the application to set this configuration explicitly but we can use "FrameBufferFetch"/"PixelLocalStorage"(16.[Bjorge 2014]) to indicate our purpose.

3-2-4-1. Vulkan

In Vulkan, one "RenderPass" consists of several "SubPass". The MSAA simple count of different attachments of the same RenderPass may not be the same. However, the MSAA sample count of the attachments refered by the same SubPass must be the same and the MSAA sample count is also expected to be the same as the count in MultisampleState of the PipelineState when issuing DrawCall.

The stochastic transparency can be implemented in one renderPass as the following: //We suppose the application doesn't turn on the MSAA for "Spatial AntiAliasing".

RenderPass  
    Attachments  
        0.FinalColor
        1.BackgroundDepth  
        2.StochasticDepth (MSAA)
        3.StochasticColor
        4.CorrectAlphaTotal
        5.StochasticTotalAlpha
    SubPasses
        0.OpaquePass
            ColorAttachments
                0.FinalColor //BackgroundColor->FinalColor
            DepthStencilAttachment
                1.BackgroundDepth
        1.CopyPass //Mentioned in StochasticDepthPass //Rasterization MSAA
            InputAttachments
                1.BackGroupDepth
            ColorAttachments
                2.StochasticDepth (MSAA)
        2.StochasticDepthPass //Rasterization MSAA
            DepthStencilAttachments
                2.StochasticDepth (MSAA)  
        3.AccumulateAndTotalAlphaPass
            InputAttachments
                2.StochasticDepth (MSAA)
            ColorAttachments
                3.StochasticColor
                4.CorrectAlphaTotal
                5.StochasticTotalAlpha
            DepthStencilAttachments
                1.BackGroupDepth
        4.CompositePass
            InputAttachments
                3.StochasticColor
                4.CorrectAlphaTotal
                5.StochasticTotalAlpha
            ColorAttachments
                0.FinalColor  //TransparentColor
                (+=(CorrectAlphaTotal×BackgroundColor))->FinalColor //implement the Over Operation by the Alpha blend hardware feature
    Dependency:
        0.SrcSubPass:0->DstSubPass:1
            //DepthStencilAttachment->InputAttachment: 1.BackGroupDepth
        1.SrcSubPass:1->DstSubPass:2
            //ColorAttachment->DepthStencilAttachment: 2.StochasticDepth (MSAA)
        2.SrcSubPass:2->DstSubPass:3
            //DepthStencilAttachment->InputAttachment: 2.StochasticDepth (MSAA)
        3.SrcSubPass:3->DstSubPass:4
            //ColorAttachment->ColorAttachment: 0.FinalColor
            //ColorAttachment->InputAttachment: 3.StochasticColor
            //ColorAttachment->InputAttachment: 4.CorrectAlphaTotal
            //ColorAttachment->InputAttachment: 5.StochasticTotalAlpha
    //SubPassDependencyChain: 0->1->2->3->4  

3-2-4-2. Metal

In Metal, there is no such thing like InputAttachment. We instead use the [color(m)]Attribute in fragment shader to read the ColorAttachment.
However, this design introduces the limit that the [color(m)]Attribute only permits us to read the ColorAttachment in the fragment shader and we have no method to read the DepthAttachment. We have to use an extra ColorAttachment to store the Depth(17.[Apple]) although this may allow us to save the bandwidth by writing the lower precise depth to the ColorAttachment and discarding the DepthAttachment. This limit may be related to the explanation of the "D3D12_RESOURCE_FLAG_DENY_SHADER_RESOURCE"(18.[Microsoft]). This means that for Apple's GPU, the performance may be improved by prohibiting reading the DepthAttachment.

Besides, there is no equivalent of "subpassInputMS" in Metal. While turning on the MSAA in Metal, the fragment shader is excuted isolatedly for each sample, we can only use the [color(m)]Attribute to read the value of one sample not all samples in the pixel and thus we can't calculate the $\operatorname{SV}( Z_i )$.

However, we may simulate the "subpassInputMS" by multiple ColorAttachments without MSAA. Since we turn off the MSAA, there exists only one sample in the DepthAttachment and thus we can't perform MSAA depth test by the hardware feature. This means that we have to simulate the depth test by programmable blending which will be explained later in the K-Buffer.

Evidently, the simulation is expected to be hostile to the performance and I don't suggest using this method in Metal.

3-2-5. Conclusion

Since MSAA is efficient on mobile GPU, the stochastic transparency is intrinsically suitable to mobile GPU. We can use the modern Vulkan API to fully explore the advantages of the mobile GPU.

However, due to the limit by the design of the Metal, I don't suggest using the stochastic transparency in Metal.

Evidently, the vertex shader doesn't read or write the ColorAttachment and thus doesn't benifit from the Tile/On-Chip Memory of the mobile GPU. The mobile GPU prefers the fragment processing to the vertex processing(10.[Harris 2019]).
The stochastic transparency still need to be improved since we still have two geometry passes(StochasticDepthPass and AccumulateAndTotalAlphaPass) which may cause the vertex processing to be the performance bottleneck.

The stochastic transparency introduces error by itself due to the random sampling while the Alpha correction eliminates the noise effectively and thus the noise impacts little.

3-2-6. Demo

The github address https://github.com/YuqiaoZhang/StochasticTransparency

The demo was originally the "StochasticTransparency" of the "NVIDIA SDK11 Samples"(9.[Bavoil 2011]). However, there are three fatal problems in the original code provide by the NVIDIA:
1."Turning on MSAA in StochasticDepthPass is to random sample and the stochastic transparency intrinsically doesn't demand other passes to turn on the MSAA." The original code provided by the NVIDIA turns on the MSAA in all passes and thus the frame rate of the stochastic transparency is unexpectedly lower than the depth peeling. I turn off all the unnecessary MSAA and the frame rate increases from 670 to 1170 while the frame rate of deep peeling is 1070.
2."The author use two separate passes AccumulatePass and TotalAlphaPass. However, we can totally merge them into a single pass." The original code provided by the NVIDIA follows the author and use two separate passes. I merge the separate passes and the frame rate increases from 1170 to 1370.
3."The depth value used in AccumulatePass is the value of the shading position not the value of the sampling position. To be consistant, we prefer to write the depth (value of the shading position) to gl_FragDepth/SV_Depth in the fragment shader." The original code provided by the NVIDIA doesn't do this. However, the Alpha correction fixes the error well and there's little impaction on the effect.

3-3. K-Buffer

Carpenter proposed the "A-Buffer" (11.[Carpenter 1984]) in the same year when Porter proposed the Alpha channel. In the A-Buffer, each pixel corresponds to a list in which all fragments corresponding to this pixel are stored. After sorting the fragments in the list by the depth, evidently we can use Over/Under operation to calculate the final color $\displaystyle C_{Final}$ .
Although A-Buffer can be implemented by UAV/StorageImage and atomic operations at present, the implementation is very tedious and inelegant. Besides, the performance of the list is low since the address of the list is not continuous and thus unfriendly to the cache. Thus there is almost no implementation in reality.

Bavoil improved the A-Buffer and proposed K-Buffer (12.[Bavoil 2007]) in 2007. In K-Buffer, we limit the number of the fragments corresponding to each pixel to no more than K. With this limit, the K-Buffer can be implemented more elegantly and efficiently.

3-3-1. RMW (Read Modify Write) Operation

In the renderpass in which we generate the K-Buffer, the following RMW operation is performed on each fragment:
1. Read: read the (at most K) fragments corresponding to the same pixel from K-Buffer
2. Modify: use the information of the current fragment and modified the (at most K) fragments which have been read from the K-Buffer
3. Write: write the (at most K) fragments which have been modified to the K-Buffer

For the current hardware, we can immediately implement the RMW operation by the UAV/StorageImage. However, things are far from simple. In general, the RMW operations performed on the fragments corresponding to the same pixel should be mutually exclusive to ensure the correctness.

Although the API guarantees the order and dependency of different draw calls, the GPU designers always tend to full explore the parallelism to improve the performance. In general, the GPU may still execute these draw calls in parallel and merely synchronize at some points.

The API doesn't guarantee the order or dependency of the executions of the fragments (corresponding to the same pixel) inside the same draw call. Evidently, the executions can be considered to be parallel since the GPU is intrinsically parallel.

The desktop GPU is "Sort-Last Fragment" (13.[Ragan-Kelley 2011]). The parallelism of the fragments is expected to be high since the synchronization occurs at the "Reorder Buffer" (13.[Ragan-Kelley 2011]) which is after the fragment shader and just before the Alpha blend.

The mobile GPU is "Tile-Based Sort-Middle" (13.[Ragan-Kelley 2011]). The executions of the fragments corresponding to the same pixel inside the same draw call can be considered to be serial (13.[Ragan-Kelley 2011]) since there doesn't exist the "Reorder Buffer". However, we shouldn't rely on this since the API doesn't guarantee that.

Bavoil proposed two hardware proposals the "Fragment Scheduling" and the "Programmable Blending" to solve this problem in 2007 (12.[Bavoil 2007]). Both two proposals have been widely supported by the hardware in reality at present.

3-3-2. Fragment Scheduling

The fragment scheduling corresponds to the RasterOrderView/FragmentShaderInterlock/RasterOrderGroup(14.[D 2015], 15.[D 2017]) at present which is generally suitable to the desktop GPU.

The pseudo code to implement the K-Buffer by the fragment scheduling is generally as the following:

    // This part of code doesn't need to be mutually exclusive
    calcalte lighting and shading ... 
                                                
    // Enter the critical section
    #if RasterOrderView // Direct3D
        read from ROV
    #elif FragmentShaderInterlock // OpenGL/Vulkan
        beginInvocationInterlockARB
    #elif RasterOrderGroup // Metal
        read from ROG
    #endif

    // This part of code is within the protection of the critical section
    perform the RMW operation on the K-Buffer ... 

    // Leave the critical section
    #if RasterOrderView // Direct3D
        write to ROV
    #elif FragmentShaderInterlock // OpenGL/Vulkan
        endInvocationInterlockARB
    #elif RasterOrderGroup // Metal
        write to ROG
    #endif

In theory, the contents which we read from or write to the ROV/ROG is not important since we merely read or write to enter/leave the critical section. Thus the proposal of "FragmentShaderInterlock" is more elegant. We don't have to read from or write to the ROV/ROG when we perform the RMW operation on the K-Buffer and the regular UAV/StorageImage(14.[D 2017]) can be used since the related code has been within the protection of the critical section.

3-3-3. Programmable Blending

The programmable blending, which is generally suitable for the mobile GPU, corresponds to the GL_EXT_shader_framebuffer_fetch extension in OpenGL, the [[color(m)]] attribute in Metal ("Table 5.5. Attributes for fragment function input arguments" of Metal Shading Language Specification) and the VK_EXT_rasterization_order_attachment_access extension in Vulkan.

The programmable blending allows the fragment shader to perform RMW as an atomic operation on the color attachment. The hardware guarantees the mutual exclusion of the fragments corresponding to the same pixel automatically.

We can enable the MRT and implement the K-Buffer by programmable blending. We assume that one pixel corresponds to four [C A Z] fragments in the K-Buffer and the related Metal code is generally as the following:

    struct KBuffer_ColorAttachment  
    {
        //In general, [[color(0)]] is used to store the CFinal
        half4 C0A0[[color(1)]]; //R8G8B8A8_UNORM
        half4 C1A1[[color(2)]]; //R8G8B8A8_UNORM
        half4 C2A2[[color(3)]]; //R8G8B8A8_UNORM
        half4 C3A3[[color(4)]]; //R8G8B8A8_UNORM
        half4 Z0123[[color(5)]]; //R16G16B16A16_FLOAT
    };
    
    struct KBuffer_Local
    {
        half4 CA[4]
        half Z[4]
    };

    fragment KBuffer_ColorAttachment KBufferPass_FragmentMain(..., KBuffer_ColorAttachment kbuffer_in)
    {
        // This part of code doesn't need to be mutually exclusive
        CA = CalcalteLighting_And_Shading(...) 
        // In general, "Z" denotes position.z
        Z = ... 

        KBuffer_Local kbuffer_local;

        // Read K-Buffer
        // We enter the critical section automatically when we read the ColorAttachment 
        kbuffer_local.Z[0] = kbuffer_in.Z0123.r; 
        kbuffer_local.Z[1] = kbuffer_in.Z0123.g;
        kbuffer_local.Z[2] = kbuffer_in.Z0123.b;
        kbuffer_local.Z[3] = kbuffer_in.Z0123.a;
        kbuffer_local.CA[0] = kbuffer_in.C0A0;
        kbuffer_local.CA[1] = kbuffer_in.C1A1;
        kbuffer_local.CA[2] = kbuffer_in.C2A2;
        kbuffer_local.CA[3] = kbuffer_in.C3A3;
        
        // Modify K-Buffer
        // This part of code is within the protection of the critical section
        ... (The concrete code depends on the requirements of the application) 
        
        // Write K-Buffer 
        // We leave the critical section automatically after we write the ColorAttachment
        KBuffer_ColorAttachment kbuffer_out;
        kbuffer_out.C0A0 = kbuffer_local.CA[0];
        kbuffer_out.C1A1 = kbuffer_local.CA[1];
        kbuffer_out.C2A2 = kbuffer_local.CA[2];
        kbuffer_out.C3A3 = kbuffer_local.CA[3];
        kbuffer_out.Z0123 = half4(kbuffer_local.Z[0], kbuffer_local.Z[1], kbuffer_local.Z[2], kbuffer_local.Z[3]); 
        
        return kbuffer_out;
    }

3-3-4. MLAB (Mult Layer Alpha Blending)

Salvi proposed three algorithms which are all based on the K-Buffer in 2010, 2011 and 2014(19.[Salvi 2010], 20.[Salvi 2011], 21.[Salvi 2014]) and we intend to explain the lastest one which is called the MLAB proposed in 2014.

3-3-4-1. K-Buffer

In MLAB, the format of the fragments in K-Buffer is [ $\displaystyle A_i C_i$ | $\displaystyle 1 - A_i$ | $\displaystyle Z_i$ ].
The algorithm is generally as the following:
1. Initializes the fragments in the K-Buffer to the "empty fragment" which is "$\displaystyle C_i$ =0 $\displaystyle A_i$ =0 $Z_i$ =farthest". // In reality, since the $\displaystyle Z_i$ is in the range from 0 to 1, we only need to ensure that the value of $\displaystyle Z_i$ is farther than all possible values.
2. When we generate the K-Buffer, the modify operation performed on the K-Buffer is to sort the fragments from near to far based on the $\displaystyle Z_i$ and insert the current fragment (which the fragment shader is executing) into the proper position based on the $\displaystyle Z_i$ .
Evidently we have K+1 fragments at present. Then the modify operation will merge the two farthest fragments into one fragment based on the rule of Under operation such that [ $\displaystyle A_i C_i$ | $\displaystyle 1 - A_i$ | $\displaystyle Z_i$ ] + [ $\displaystyle A_{i+1} C_{i+1}$ | $\displaystyle 1 - A_{i+1}$ | $\displaystyle Z_{i+1}$ ] = [ $\displaystyle A_i C_i + ( 1 - A_i ) A_{i+1} C_{i+1}$ | $\displaystyle ( 1 - A_i ) ( 1 - A_{i+1} )$ | $\displaystyle Z_i$ ] and thus we have K fragments again.
Evidently, if we insert another fragment nearer than the fragment merged by two fragments, there exists error. By Salvi, the error intruduced by the two farthest fragments is the lowest since the visibility function $\displaystyle \operatorname{V} ( Z_i )$ is monotonically decreasing and the farthest fragments generally introduce the lowest error.
3. Based on the generated K-Buffer, we calculate the total contribution of the transparent geometries to the final color $\displaystyle C_{Final}$ by the K fragments.

3-3-4-2. Render Pass

1. OpaquePass
draw the opaque geometries and have the BackgroundColor and the BackgroundDepth.

2. KBufferPass // GeometryPass
reuse the BackgroundDepth by the OpaquePass
use clear load_op to initilize the fragments in the K-Buffer to the "empty fragment" [ 0 0 farthest]
with depth test without depth write, sort the transparent geometries by [material] and draw them to generate the K-Buffer
Note that since the depth write is turned off, the order of the geometries doesn't impact on the performance and thus we sort the geometries only by the material.

3. CompositePass // FullScreenTrianglePass
Based on the generated K-Buffer, use the Under operation to calculate the total contribution of the transparent geometries to the final color $\displaystyle C_{Final}$ : TransparentColor and AlphaTotal

Then, add the TransparentColor to the final color $\displaystyle C_{Final}$ by the Over Operation:
$\displaystyle C_{Final}$ = TransparentColor + CorrectAlphaTotal × BackgroundColor)
Note that the BackgroundColor has been added to the color buffer. We can output the TransparentColor and CorrectAlphaTotal in the fragment shader and use the Alpha blend hardware feature to implement the Over Operation.

3-3-5. Tile/On-Chip Memory

The K-Buffer is intrinsically suitable to mobile GPU.

In the traditional desktop GPU, the bandwidth is increased by K times due to the K-Buffer.

However, in the mobile GPU, we can keep the K-Buffer in the Tile/On-Chip Memory and discard the K-Buffer when the renderpass ends without writing to the main memory. This means that the bandwidth can be decreased to almost zero.

3-3-5-1. Vulkan

The K-Buffer can be implemented by the VK_EXT_rasterization_order_attachment_access extension in Vulkan.

However, this extension has not been widely supported on Android devices.

3-3-5-2. Metal

The K-Buffer can be implemented in one renderPass as the following: // We assume that the K of K-Buffer equals four.

    RenderPassDescriptor:
        ColorAttachment:
            0.FinalColor // Load:Clear // Store:Store // Format:R10G10B10A2_UNORM  // HDR10
            1.xyz:A0*C0 w:1-A0 //Load:Clear // ClearValue:[ 0 0 0 1 ] //Store:DontCare //Format:R16G16B16A16_FLOAT  
            // The size of the PixelStorage is limited(A7-128bit A8\A9\A10-256bit A11-512bit)  
            // Since the visibility function is monotonically decreasing and the farther fragments generally contribute introduce the lowest error, we prefer to reduce the precision of the farther fragments.
            2.xyz:A1*C1 w:1-A1 // Load:Clear // ClearValue:[ 0 0 0 1 ] // Store:DontCare // Format:R8G8B8A8_UNORM 
            3.xyz:A2*C2 w:1-A2 // Load:Clear // ClearValue:[ 0 0 0 1 ] // Store:DontCare // Format:R8G8B8A8_UNORM
            4.xyz:A3*C3 w:1-A3 // Load:Clear // ClearValue:[ 0 0 0 1 ] // Store:DontCare // Format:R8G8B8A8_UNORM
            5.Z0123 // Load:Clear // ClearValue:[ farthest farthest farthest farthest ] // Store:DontCare // Format:R16G16B16A16_FLOAT
        DepthAttachment:
            Depth // Load:Clear // Store:DontCare
    RenderCommandEncoder:
        0.OpaquePass:
            BackgroundColor->Color[0]
            BackgroundDepth->Depth
        1.KBufferPass:
            Read: Color[1]/Color[2]/Color[3]/Color[4]/Color[5] -> 4 Fragments
            Modify: ...
            Write: 4 Fragments -> Color[1]/Color[2]/Color[3]/Color[4]/Color[5]
            // reuse the BackgroundDepth
        3.CompositePass:
            Color[1]/Color[2]/Color[3]/Color[4]/Color[5] -> ...
            ... -> TransparentColor
            ... -> AlphaTotal
            Color[0] -> BackgroundColor
            TransparentColor+AlphaTotal*BackgroundColor -> Color[0]

3-3-6. Conclusion

Since the K-Buffer is efficient on mobile GPU, the MLAB is intrinsically suitable to mobile GPU. We can use the modern Metal API to fully explore the advantages of the mobile GPU.

Compared to the stochastic transparency, there is only one geometry pass in MLAB. This is beneficial to the mobile GPU since the vertex processing is not efficient on the mobile GPU.

Besides, for the mobile GPU, the executions of the fragments corresponding to the same pixel inside the same draw call is intrinsically serial (13.[Ragan-Kelley 2011]) and thus the mutual exclusion can be considered to introduce little overhead.
However, for the desktop GPU, mutual exclusion of the RMW operation limits the parallelism of the fragments and introduces extra overhead which is related to the "Depth Complexity" of the scene.

When we insert another fragment nearer than the fragment merged by two fragments, we introduce error.
However, since the visibility function $\displaystyle \operatorname{V} ( Z_i )$ is monotonically decreasing, the farthest fragments generally introduce little error and thus the error impacts little.

3-3-7. Demo

The github address https://github.com/HanetakaChou/MultiLayerAlphaBlending

The demo was originally the "Order Independent Transparency with Imageblocks" of the "Metal Sample Code"(22.[Imbrogno 2017]). However, the original code provide by the Apple depends on the feature Imageblock which is only available on A11 and later GPU. The Imageblock is intrinsically to customize the format of the framebuffer which is not related to the mutual exclusion of the RMW operation at all. Thus I have modified the demo and use the \[[Color(m)]] Attributeto implement the related code and the demo can be run on A8 and later GPU.

The relationship of the features between Metal and OpenGL:
\[[Color(m)]] Attribute <-> FrameBufferFetch // To support the programmable blending
ImageBlock <-> PixelLocalStorage // To customize the format of the framebuffer

3-4. Weighted Blending

The estimation of the visibility function $\displaystyle \operatorname{V} ( Z_i )$ depends on the order of the fragments. This results in that the estimation of the final color $\displaystyle C_{\displaystyle Final} = \sum_{\displaystyle i = 0}^{\displaystyle n} \operatorname{V} ( Z_i ) A_i C_i$ depends on the order.
Also by this fact, McGuire proposed the "Weighted Blending"(23.[McGuire 2013], 4.[Dunn 2014]) in 2013 which uses a predefined weighted function $\displaystyle \operatorname{W}( EyeSpaceZ_i, A_i)$ which is evidently order independent to simulate the visibility function $\operatorname{V} ( Z_i )$.

3-4-1. Weighted Function

By McGuire, the nearest fragments might contribute too much to the final color if the weighted function only depended on the $EyeSpaceZ_i$ . Thus the weighted function depends on both the $EyeSpaceZ_i$ and the $A_i$ .

Besides, McGuire proposed three suggested weighted function as the following:
1.${\operatorname{W}( EyeSpaceZ_i,A_i)}=\operatorname{clamp}{({\frac{10.0f}{0.00001f+{(\frac{EyeSpaceZ_i}{5.0f})}^{2.0f}+{(\frac{EyeSpaceZ_i}{200.0f})}^{6.0f}}},0.01f,3000.0f)}*A_i$
2.${\operatorname{W}( EyeSpaceZ_i,A_i)}=\operatorname{clamp}{({\frac{10.0f}{0.00001f+{(\frac{EyeSpaceZ_i}{10.0f})}^{3.0f}+{(\frac{EyeSpaceZ_i}{200.0f})}^{6.0f}}},0.01f,3000.0f)}*A_i$
3.${\operatorname{W}( EyeSpaceZ_i,A_i)}=\operatorname{clamp}{({\frac{0.03f}{0.00001f+{(\frac{EyeSpaceZ_i}{200.0f})}^{4.0f}}},0.01f,3000.0f)}*A_i$
Verified by McGuire, the effect seems good when the $EyeSpaceZ_i$ is in the range from 0.1 to 500 and the precision of the $EyeSpaceZ_i$ is half float.
Note that the weighted function may exceed 1 when the fragment is very near while the visibility function is evidently less or equal than 1.

3-4-2. Normalization

We have proved that ${\displaystyle{\sum_{i = 0}^n}} ( \operatorname{V} ( Z_i ) A_i ) = 1 - {\displaystyle{\prod_{i = 0}^n}} ( 1 - A_i )$ in Alpha correction.

The normalization means that we assume that $\frac{\operatorname{W}(EyeSpaceZ_i,A_i)}{{\displaystyle\sum_{i = 0}^n}(\operatorname{W}(EyeSpaceZ_i,A_i) A_i)} = \frac{\operatorname{V}( Z_i)}{{\displaystyle\sum_{i = 0}^n}(\operatorname{V}( Z_i) A_i)}$ and we have that ${\operatorname{V}( Z_i )} = {\operatorname{W}( EyeSpaceZ_i,A_i)}{\frac{{\displaystyle\sum_{i = 0}^n}(\operatorname{V}( Z_i) A_i)}{{\displaystyle\sum_{i = 0}^n}(\operatorname{W}( EyeSpaceZ_i,A_i) A_i)}} = {\operatorname{W}(EyeSpaceZ_i,A_i)}{\frac{1-{\displaystyle\prod_{i = 0}^n}( 1 - A_i )}{{\displaystyle\sum_{i = 0}^n}(\operatorname{W}(EyeSpaceZ_i, A_i) A_i)}}$.

3-4-3. Render Pass

1.OpaquePass
draw the opaque geometries and have the BackgroundColor and the BackgroundDepth.

2.AccumulateAndTotalAlphaPass //GeometryPass initilize the depth with the BackgroundDepth
with depth test without depth write, sort the transparent geometries by [material] and draw them, having WeightedColor=$\displaystyle \sum_i{({\operatorname{W}( EyeSpaceZ_i,A_i)}A_iC_i)}$, CorrectAlphaTotal= $1-\prod_i( 1-A_i)$ and WeightedTotalAlpha=$\sum_i{({\operatorname{W}( EyeSpaceZ_i,A_i)}A_i)}$
Note that:
1.Since the depth write is turned off, the order of the geometries doesn't impact on the performance and thus we sort the geometries only by the material.
2.The relationship between the AlphaTotal and the TotalAlpha is TotalAlpha = 1 – AlphaTotal as stated in the stochastic transparency.

3.CompositePass //FullScreenTrianglePass
The total contribution of the transparent geometries:
TransparentColor=$\displaystyle \sum_i{({({\operatorname{W}( EyeSpaceZ_i,A_i)}\frac{1-\prod_i( 1-A_i)}{\sum_i({\operatorname{W}( EyeSpaceZ_i,A_i)}A_i)})}A_iC_i)}={(\sum_i{\operatorname{W}( EyeSpaceZ_i,A_i)}A_iC_i)}{\frac{1-\prod_i( 1-A_i)}{\sum_i({\operatorname{W}( EyeSpaceZ_i,A_i)}A_i)}}=WeightedColor\frac{1-CorrectAlphaTotal}{WeightedTotalAlpha}$

Then, add the TransparentColor to the final color $\displaystyle C_{Final}$ by the Over Operation:
$\displaystyle C_{Final}$ = TransparentColor + CorrectAlphaTotal × BackgroundColor)
Note that the BackgroundColor has been added to the color buffer. We can output the TransparentColor and CorrectAlphaTotal in the fragment shader and use the Alpha blend hardware feature to implement the Over Operation.

3-4-4. Conclusion

The weighted blending uses the predefined weighted function$\displaystyle \operatorname{W}( EyeSpaceZ_i, A_i)$ to simulate the visibility function $\operatorname{V} ( Z_i )$ , omitting the calculation of the visibility function.
To some extent, the weighted blending is considered as a simplified version of the stochastic transparency which omits the StochasticDepthPass.
Consequently, the error of the weighted blending is highest of all OIT algorthims since the weighted function $\displaystyle \operatorname{W}( EyeSpaceZ_i, A_i)$ which is used to simulate the visibility function $\operatorname{V} ( Z_i )$ is not related to the scene at all.

3-4-5. Demo

The github address https://github.com/YuqiaoZhang/WeightedBlendedOIT

The demo was originally the "Weighted Blended Order-independent Transparency" of the "NVIDIA GameWorks Vulkan and OpenGL Samples"(24.[NVIDIA]). The weighted blended is the simplest of the all OIT algorithms and I haven't made any substantial changes to the demo.

4. References

1.[Porter 1984] Thomas Porter, Tom Duff. "Compositing Digital Images." SIGGRAPH 1984.
2.[Yusor 2013] Egor Yusor. "Practical Implementation of Light Scattering Effects Using Epipolar Sampling and 1D Min/Max Binary Trees." GDC 2013. First-Edition Second-Edition Third-Edition
3.[Hoobler 2016] Nathan Hoobler. "Fast, Flexible, Physically-Based Volumetric Light Scattering." GDC 2016.
4.[Dunn 2014] Alex Dunn. "Transparency (or Translucency) Rendering." NVIDIA GameWorks Blog 2014.
5.[Everitt 2001] Cass Everitt. "Interactive Order-Independent Transparency." NVIDIA WhitePaper 2001.
6.[Enderton 2010] Eric Enderton, Erik Sintorn, Peter Shirley, David Luebke. "Stochastic Transparency." SIGGRAPH 2010.
7.[Laine 2011] Samuli Laine, Tero Karras. "Stratified Sampling for Stochastic Transparency." EGSR 2011.
8.[McGuire 2011] Morgan McGuire, Eric Enderton. "Colored Stochastic Shadow Maps". SIGGRAPH 2011.
9.[Bavoil 2011] Louis Bavoil, Eric Enderton. "Constant-Memory Order-Independent Transparency Techniques." NVIDIA SDK11 Samples / StochasticTransparency 2011.
10.[Harris 2019] Pete Harris. "Arm Mali GPUs Best Practices Developer Guide." ARM Developer 2019.
11.[Carpenter 1984] Loren Carpenter. "The A-buffer, an Antialiased Hidden Surface Method." SIGGRAPH 1984.
12.[Bavoil 2007] Louis Bavoil, Steven Callahan, Aaron Lefohn, Joao Comba, Claudio Silva. "Multi-fragment Effects on the GPU using the k-Buffer." SIGGRAPH 2007.
13.[Ragan-Kelley 2011] Jonathan Ragan-Kelley, Jaakko Lehtinen, Jiawen Chen, Michael Doggett, Frédo Durand. "Decoupled Sampling for Graphics Pipelines." ACM TOG 2011.
14.[D 2015] Leigh D. "Rasterizer Order Views 101: a Primer." Intel Developer Zone 2015.
15.[D 2017] Leigh D. "Order-Independent Transparency Approximation with Raster Order Views (Update 2017)." Intel Developer Zone 2017.
16.[Bjorge 2014] Marius Bjorge, Sam Martin, Sandeep Kakarlapudi, Jan-Harald Fredriksen. "Efficient Rendering with Tile Local Storage." SIGGRAPH 2014.
17.[Apple] Metal Sample Code / Deferred Lighting
18.[Microsoft] Direct3D 12 Graphics / D3D12.h / D3D12_RESOURCE_FLAGS enumeration
19.[Salvi 2010] Marco Salvi,Kiril Vidimce, Andrew Lauritzen, Aaron Lefohn. "Adaptive Volumetric Shadow Maps." EGSR 2010.
20.[Salvi 2011] Marco Salvi, Jefferson Montgomery, Aaron Lefohn. "Adaptive Transparency." HPG 2011.
21.[Salvi 2014] Marco Salvi, Karthik Vaidyanathan. "Multi-layer Alpha Blending." SIGGRAPH 2014.
22.[Imbrogno 2017] Michael Imbrogno. "Metal 2 on A11 – Imageblocks." Apple Developer 2017.
23.[McGuire 2013] Morgan McGuire, Louis Bavoil. "Weighted Blended Order-Independent Transparency. " JCGT 2013.
24.[NVIDIA] NVIDIA GameWorks Vulkan and OpenGL Samples / Weighted Blended Order-independent Transparency